
現在の素粒子物理学の模型の理論的枠組は場の量子論によって与えられています。 特に,素粒子間の基本相互作用,つまり電磁気力と弱い力,強い力(,及び重力),はゲージ理論で記述されると信じられています。 標準的には,相互作用が弱いと仮定して計算しやすい理論から展開する「摂動計算」による予言と実験結果が一致することから,素粒子の模型の妥当性が検証されてきました。 しかし,非可換群のゲージ理論であるYang-Mills理論は電弱相互作用や強い相互作用を記述するのに用いられるが,Yang-Mills理論の低エネルギーでは,標準的な摂動計算では取り込めない非摂動効果が重要になってくることが知られています。 特に,強い相互作用[a]には「カラー閉じ込め」,つまりカラーを持った クォークやグルーオンなどは観測されず,カラーを持たない陽子や中性子といった形でしか観測されない,という重要な特徴があります。 場の量子論の枠組みではこの閉じ込め機構は解明されていません。 これは,Yang-Mills理論の基本的な励起であるグルーオンなどが観測されないといった,ゲージ理論の非常に基本的な特徴すら説明されていないことを意味します。 素粒子の基本相互作用はゲージ理論で記述されることを鑑みると,カラー閉じ込めの問題は物理学の最も重要な課題の1つであると言えます。 我々はこのカラー閉じ込め機構の理解を目指して,研究を行っています。
伝播関数 (2点相関関数) とは,場の量子論の重要な関数の1つです。これは,大雑把にいって,「真空に場の演算子を作用させた状態」と,「その状態を時間・空間並進させた状態」との内積 (遷移振幅) のことです。通常の場合,「真空に場の演算子を作用させた状態」というのは,対応する粒子の状態におおよそ対応するので,非常に大雑把にいえば伝播関数は「「粒子」のある場所・時間から別のある場所・時間への確率振幅」を与える関数と言えます。 この関数が非常に重要である理由は,その関数の解析的構造が「場に関係する状態の情報 (特にエネルギー・運動量スペクトル)」を教えてくれることにあります。
伝播関数をフーリエ変換したもの (運動量表示の伝播関数) を解析接続して得られる複素解析的な特異性 (極や不連続性) は,場に関係する状態に対応します。
より具体的には,運動量 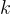 の関数である伝播関数は,Lorentz対称性から,
の関数である伝播関数は,Lorentz対称性から,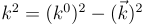 の関数で書けますが,複素
の関数で書けますが,複素 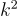 平面での極が一粒子状態に、分岐切断が多粒子状態に対応します。また,その極の位置はその一粒子状態の質量の二乗を表します。
通常の場の量子論では, 伝播関数はKällén–Lehmann表示に従い,
平面での極が一粒子状態に、分岐切断が多粒子状態に対応します。また,その極の位置はその一粒子状態の質量の二乗を表します。
通常の場の量子論では, 伝播関数はKällén–Lehmann表示に従い,  にのみ特異性を持ちます。
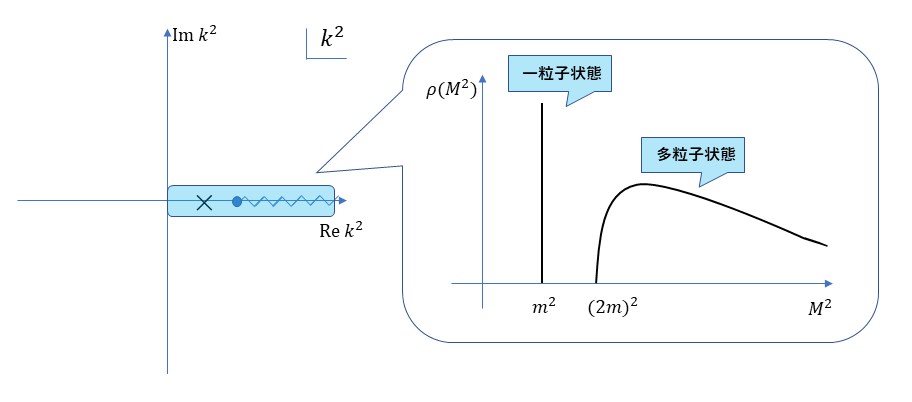
この特異性を特徴づける関数をスペクトル関数といい,場に対応する状態のエネルギースペクトルを表します (図1参照)。
にのみ特異性を持ちます。
この特異性を特徴づける関数をスペクトル関数といい,場に対応する状態のエネルギースペクトルを表します (図1参照)。
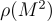
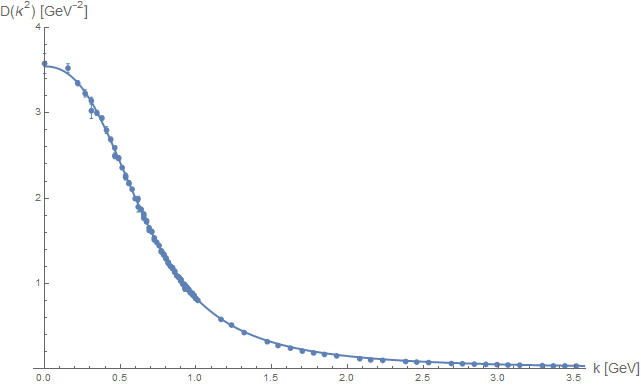
有質量Yang-Mills模型とは,いくつかの動機に基づいてLandauゲージの通常のYang-Mills理論に変形を施した模型です。 この模型では,驚くべきことに,簡単な摂動計算でグルーオン等の伝播関数の格子計算 (数値シミュレーション) [b]の結果を再現します (図2参照)。 その上,通常のYang-Mills理論と異なり,「摂動論が低エネルギーでも明白には破綻しない」ことが言えます。
先に述べた,格子計算を再現する「有質量Yang-Mills模型で最低限の量子補正を加えたグルーオン伝播関数」を,複素 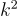 平面に解析接続すると,図1の通常の場の量子論の解析的構造に反して,複素極が出現します (図3参照) [1]。
平面に解析接続すると,図1の通常の場の量子論の解析的構造に反して,複素極が出現します (図3参照) [1]。
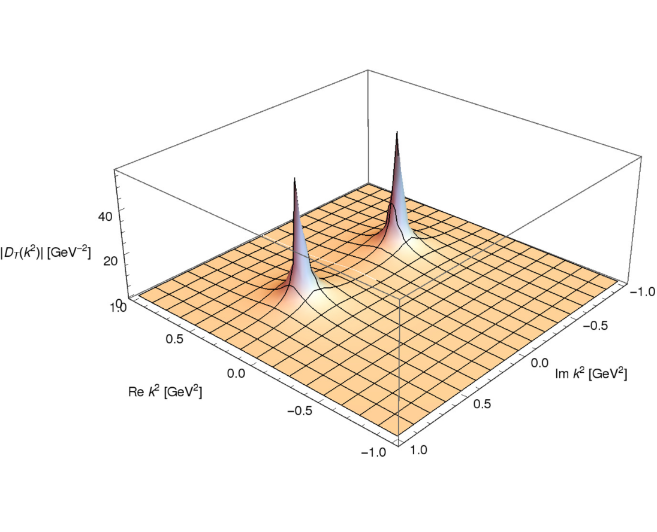
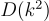 を複素平面に解析接続した関数の絶対値。複素共役な一対の極の存在が見える。
を複素平面に解析接続した関数の絶対値。複素共役な一対の極の存在が見える。
また,我々はスペクトル関数の符号と複素極の数の間にある一般的関係を導出しました。実は,それを用いて「有質量Yang-Mills模型で最低限の量子補正を加えたグルーオン伝播関数」はパラメータによらずこのような複素極が出現することが示せます。これを用いた更なる発展として,ゲージヒッグス系と有質量Yang-Mills模型の類似性を通したゲージヒッグス系への応用[2],クォークを加えた系での複素極の数の調査[3] などがあります。
複素極は通常の場の量子論の枠組みでは禁止されているものなので,そのような特異性を持つ理論は一切物理的な解釈ができないのでしょうか? 一方で,近年,我々の研究のみならず,独立な手法で複素領域での特異性を示唆する研究がいくつか現れてきています。 そのため,複素極の解釈を考えることは非常に重要と言えます。 よって,我々は公理論的場の量子論の観点を用いて,複素極を持つ理論の一般的性質と,その解釈を調べました。その結果,次の性質が厳密に成り立つことが分かりました。
我々は,主に,(1) 模型を使った複素極の予言 と (2) 複素極を持つ理論の一般的性質の検討 を行いました。今後,これらの結果をもとに,伝播関数の解析的構造の視点から,カラー閉じ込め機構の理解が進むことを期待しています。
この研究は, 科学研究費補助金 JSPS Research Fellowship for Young Scientists Grant No.20J20215, および,Grant-in-Aid for Scientific Research, JSPS KAKENHI Grant (C) No.19K03840 の支援を受けています.