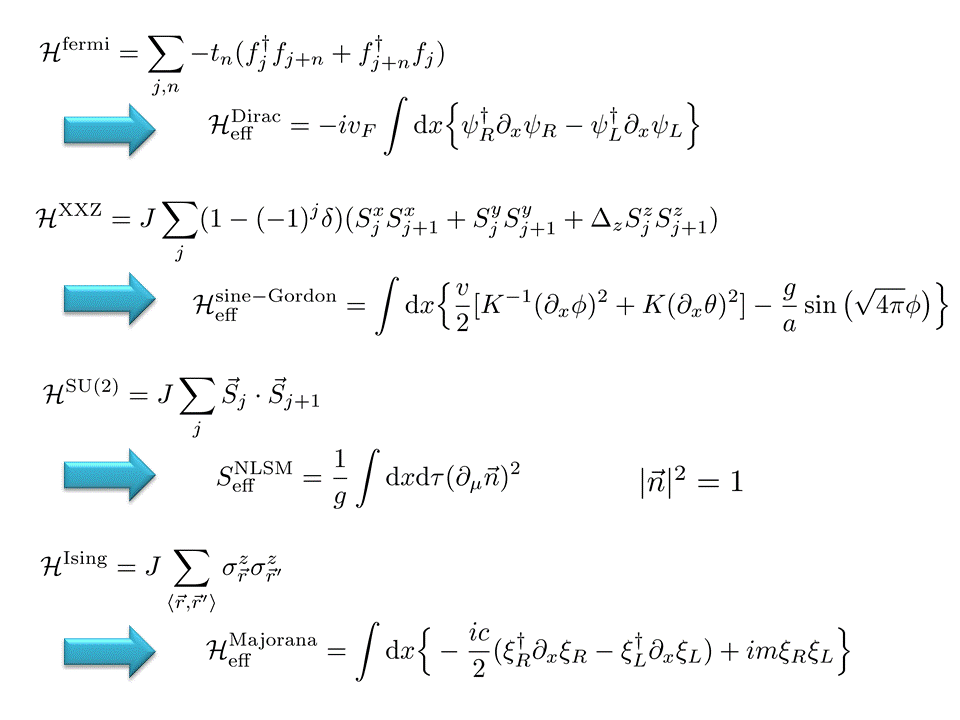研究内容
佐藤は、これまで主に多体系(膨大な数の単純な構成要素から成る系)が示す普遍的または
特徴的な物理現象を理論物理学的方法を用いて探索・予言・解明してきました。研究内容はおおよそ
物性理論・統計物理学と呼ばれる分野に属しますが、これらの分野に対する帰属意識に縛られず、
独創性のある新しい成果・さらには新しい分野・概念・理論の構築を目指していきたいと考えています。
平たく換言すると、流行を必死に後追いすることは避け(ある程度流れに乗ることも大事ですが)、
自らのアイディアに基づいた新しい研究成果を目指します、ということになります。
研究を生業としていることへの感謝の念を忘れずに、研究活動に打ち込んでいきたいと思います。
自然科学は(特に20世紀以降)猛烈な勢いで発展しその研究対象は拡大を続けていますが、
それを分類する1つの方法は対象とする系のサイズ(スケール)による分類法です。
各々のスケール(階層)に普遍的な法則が存在することがこれまでの科学研究で経験的に分かっています。
物性科学・統計物理学は、素粒子・原子核物理学の世界より大きな原子分子のスケール
(オングストローム~ナノメートル)から人間程度のスケール(メートル)で生じる現象を主要な研究対象としています。
科学研究は人間によって行われる為、人間のスケールを含むこの物性科学-特に固体物性研究-は他の階層の自然科学より
実験研究の遂行が容易(あくまでも他の階層と比べて)であり、
それ故、20世紀にもっとも発展・精密化した科学分野の1つと言って良いでしょう。
物性科学・統計物理学は、理論と実験が相互作用しながら発展させることができる理想的な
自然科学分野の1つと言えます。このような性質から、物性科学では、
物理学の普遍性と多様性の両方を日常的に感じ取ることができます!
物性・統計物理分野の中で佐藤はとりわけ磁性についての研究経験が多い為、
その知識がしばしば拠り所になります。磁性体模型は他の多体系模型と比べて一般に単純ですが、不思議なことに、
実験を定量的に説明する能力も備えています。これは、素粒子論(高エネルギー極限)とは逆の
低エネルギーにおける普遍性の表れとも言えるでしょう。そのような逆極限において、
素粒子論の武器である場の理論が有効性を発揮することも面白いところです。
系の単純さ故、磁性理論分野においては、場の理論に加えて、
代表的な模型に対する精密で深い数理構造や多彩な解析方法が解明・発展しています。
最近では理論から予言される美しい数理構造が実際の実験で観測されることも珍しくありません。
また磁性理論と他分野(数理物理、素粒子論、共形場理論、可積分系、トポロジー、情報理論など)とのつながりも
深く発展しています。これらの知識を心の故郷としながら、より広い分野で研究活動をしています。
歴史のある物理分野の知識や考え方は周辺分野でも強力な武器になります。
さらに新しい開拓地の新しい現象を理解する際も、
磁性の知識が比較対象を与え、より深い理解へつながることがあるのです。
最近、佐藤は「スピントロニクス」「非平衡量子系」「磁気光学」「熱・電磁気効果」「時間依存外場による量子状態の制御・生成」「フロッケ・エンジニアリング」「散逸量子系」
「マルチフェロイクス」「カイラリティ」などのキーワードに焦点を当てて研究を遂行しています。
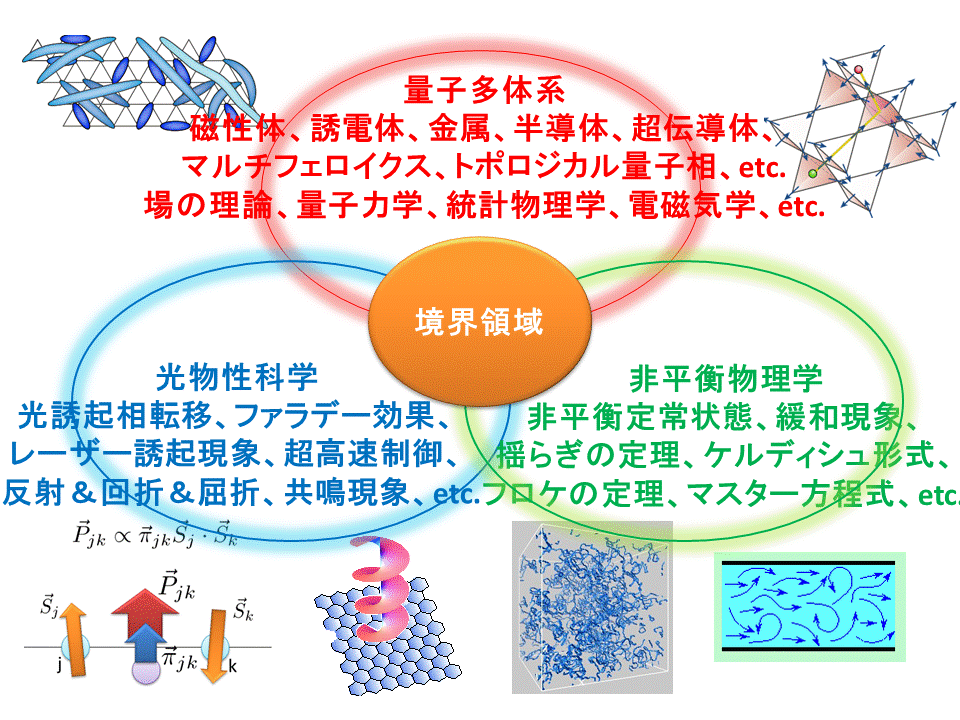
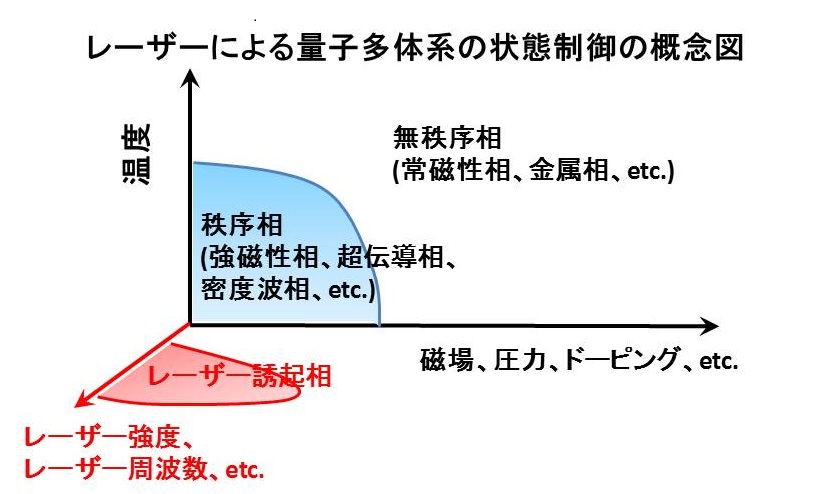
これらのキーワードで特徴づけられる研究テーマは、しばしば今までの物性科学の各分野の中で学際・境界領域に位置しています(右図)。
このような新しい領域では、多くの解決すべき重要な科学的問題を発掘することが可能です。
同時に、その問題解決には複数の分野についての知識が要求されます。
上のキーワードで特徴づけられるような新しい分野を開拓し、教科書に載るような成果を目指していくつもりです。
特に、新しい物理現象の発見・物質の持つ機能を最大化(最適化)させる、ということに拘った研究をしていきたいと考えています。
より具体的な今までの研究成果や今後の目標については、以下で、分野毎に分けて解説します
(現在進行中の研究については、紹介内容を制限しています)。
以下に紹介する内容の多くは、様々な研究者の方々との共同研究により得られた成果です。
最近の研究成果の更新をさぼっています。そのうち、よりわかりやすく分類された研究成果を解説したページで以下を置換します。
私の研究内容に興味を持っていただける若手研究者(若くなくても)がいれば、大変うれしく思います。
私の主観的な研究に対する考え方などについては次のページをご覧ください。
超高速スピントロニクス・磁気光学・マルチフェロイクスの電気磁気効果
ここ10年ほどの間に、スピントロニクスと関連する科学は著しく発展しています。スピントロニクスとは、
エレクトロニクス(電子工学)の科学・技術に電子スピン自由度も巧みに組み込んで革新的な情報処理法を発展させることを
目指した科学(工学)分野です。スピントロニクスの最終目標が「社会への新技術の応用」であることもあり、
理学よりも工学寄りの研究者が多数研究に携わっています。
それ故、理学工学両方を巻き込んで大きな発展が継続しており、また同様の理由で実験研究が分野を牽引しており、
その意味で健全な自然科学分野とも言えます。
スピントロニクスでは、マクロスケール又はメソスケールの物質中の磁化やスピン流(スピン角運動量の流れ)などの
スピン自由度と関連する物理量の生成・制御が中心的テーマの1つと言えます。
この生成・制御の方法として、最近我々はレーザー光(電磁波)を磁性体に照射する新しい方法を
理論的に提案することに成功しています。
レーザーを利用する利点の1つは、レーザー光が非常に高速なスピンダイナミクスを誘導できる、という点です。
例えば、可視光のレーザーパルスは1fs(フェムト秒:10^{-15}秒)オーダーの間だけ系に電磁場を与え揺さぶるのです。
以下、3つの成果について簡単に紹介します。現在も新しいアイディアに基づいた研究が進行中です。

(A1)円偏光レーザーによる量子磁性体の磁化生成・制御
磁性体にレーザー光を照射して磁化を変化させる研究は、10年以上前から精力的に行われています。
そこでは一般に可視光周りの周波数帯のレーザーが利用されます。
可視光レーザー技術は非常に発展しており、可視光で磁性体を制御しようとする試みは自然な研究の潮流と言えるでしょう。
しかしながら、スピンダイナミクスのエネルギースケールと可視光の光子エネルギーのスケールがかけ離れている為、
その理論を構築するのは非常に難しく、実際、実験で実現している可視光による磁化の変化を説明する理論はまだまだ未成熟です。
一方、最近テラヘルツ(THz)帯のレーザー技術が急速に発展してきており、THz帯の光子エネルギーはまさに磁性体の磁気励起と
同じ程度のエネルギースケールに対応します。すなわち、THzレーザー中の磁性体の問題は、ハミルトニアンを用いて
微視的に解析することが原理的に可能と言えます。そこで我々は、微視的なハミルトニアンに基づく量子論的解析から、
周波数をゆっくり増加させながら(チャーピング)THz領域の円偏光レーザーを磁性絶縁体に照射すると、
平衡磁化過程とほぼ同じ磁化曲線が「時間」の関数として得られることを明らかにしました。
さらに具体的な磁性体模型を解析することでトポロジカルな性質を持つ磁化プラトー状態もレーザー照射で生成可能であることも示しました。
これらの結果は静磁場を用いずに磁化を制御する新しい方法の提案といえます。
角運動量保存の観点から上の現象を考察すると、光子の角運動量が磁性体の電子スピンに転写されていると解釈できます。
一方、力学的角運動量と電子スピン角運動量の間の転写現象はアインシュタイン以来良く知られており、
アインシュタイン・ドハース効果(スピン→力学回転:右上図)とバーネット効果(力学回転→スピン:左図)と呼ばれています。
従って我々の予言は、レーザー版のバーネット効果ということができます。(アニメーション:原子力機構松尾衛氏提供)
S. Takayoshi, M. Sato, and T. Oka,
Phys. Rev. B 90, 214413 (2014)
M. Sato, Y. Yoshimoto, and N. Furukawa, in preparation.
佐藤、高吉、岡:日本物理学会2017年11月号に解説記事「レーザー駆動超高速スピントロニクスとフロケエンジニアリング」
(A2)マルチフェロイクスにおける円偏光レーザーを利用した超高速スピン流生成方法:レーザーで磁石をひねる!
ここ10年ほどの間、スピントロニクスとは独立に(しかしながら結果的に関連して)マルチフェロイクスの研究が精力的に行われてきました。
マルチフェロイクス(強誘電磁性体)とは、磁気自由度と電気分極自由度が強く結合した一連の強誘電性を示す磁性絶縁体であり、
この物質群では、磁性と誘電性の興味深い相関現象(交差相関効果、電気磁気効果と呼ばれます)が生じます。マルチフェロイクスは
電気分極を介して電磁波の磁場成分だけでなく電場成分にも応答し、この性質が普通の磁性絶縁体との決定的な違いと言えます。
これまで多様なマルチフェロイクスが発見・合成されていますが、
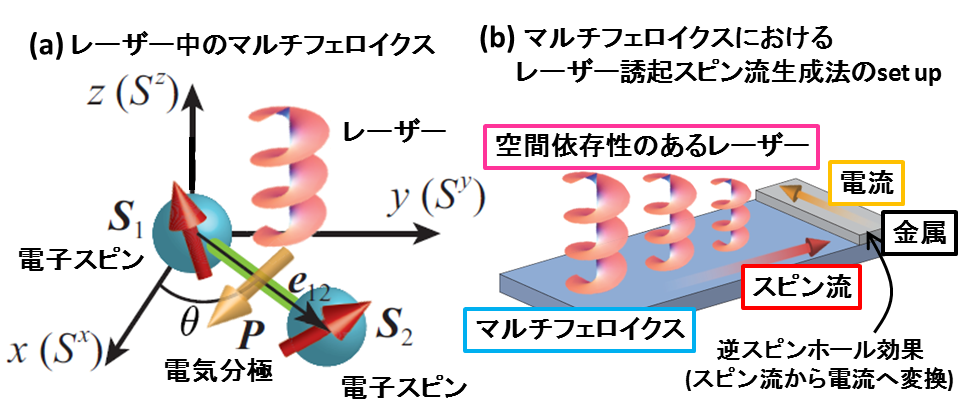
電気分極が近接する電子スピンの外積で定義されるスピンカイラリティ(S×S)と結合する一連のマルチフェロイクスはその代表例です。
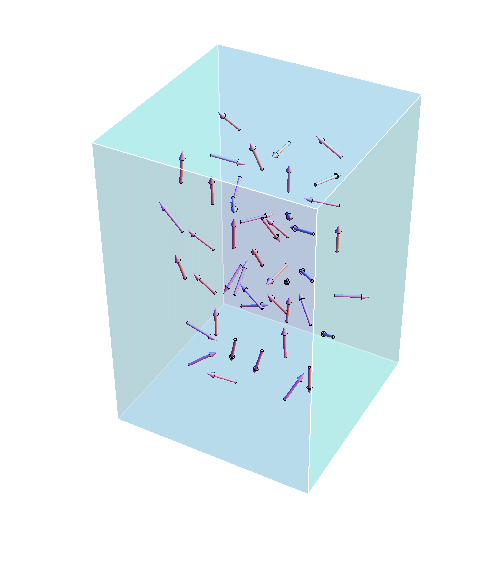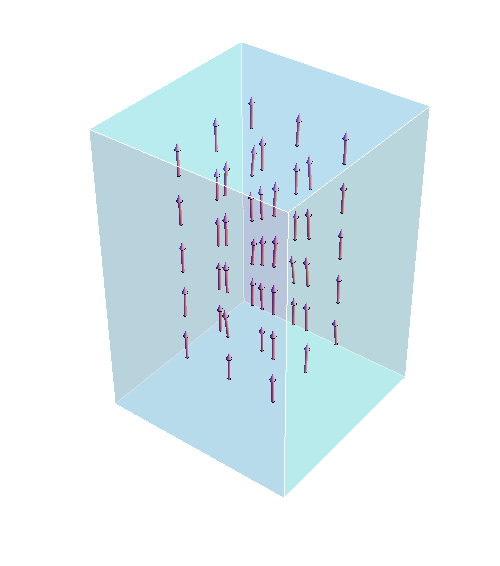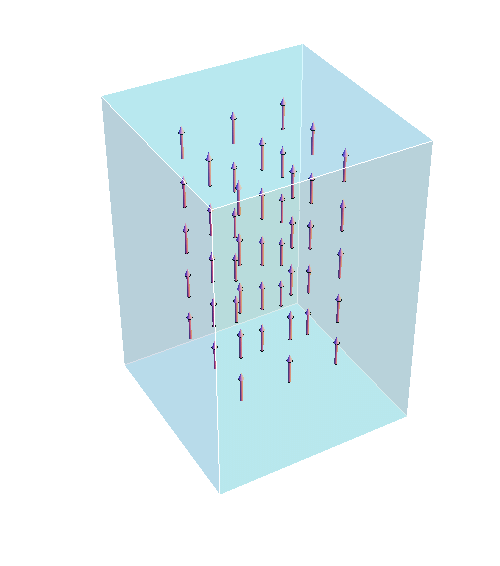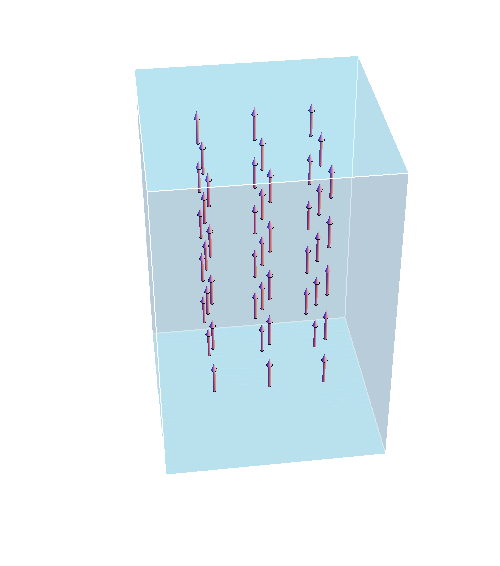
我々は、このクラスのマルチフェロイクスにTHz円偏光レーザーを照射することで、新しいジャロシンスキー守谷(DM)相互作用が系の中に
発現することをフロケ理論と数値解析を組み合わせることで明らかにしました。DM相互作用は一般に捻られたスピンの空間構造を誘導し
それは瞬間的なスピン流の生成を示唆しています。我々は、空間的に変調したTHz円偏光レーザーをマルチフェロイクスに照射することで
実際にスピン流が生成され得ることも明らかにしました。これは新しいスピン流生成方法の提案と言えます。
M. Sato, S. Takayoshi, and T. Oka,
Phys. Rev. Letts. 117, 147202 (2016)
茨城大解説ページ
佐藤、高吉、岡:日本物理学会2017年11月号に解説記事「レーザー駆動超高速スピントロニクスとフロケエンジニアリング」
(A3)光渦のミクロ物性への応用:光渦による新しいトポロジカル磁気欠陥の超高速生成・制御
光渦とは軌道角運動量をもった電磁波(レーザー)であり、近年広い周波数領域で実現しています。
同様にして、電子線版の光渦も存在します。通常のレーザーでは、その進行方向に垂直な面を見たとき
中心部から動径方向に向かってレーザー強度が単調に低下していきますが、光渦の電磁場強度は
リング状(多重リングも含む)の分布を持ちます。
このような光渦の特性(軌道角運動量や空間非一様性)から、その多様な応用が期待されていますが、
これまでの光渦の研究の多くはある程度マクロな現象(マイクロメートル以上)を対象としており、
固体電子物性を対象とした微視的な応用の可能性は十分考察されていませんでした。
カイラル磁性体では、交換相互作用とジャロシンスキー守谷相互作用の競合によりナノスピンテクスチャが
しばしばエネルギー的に安定に生存できます。
例えば2次元カイラル磁性体で安定に存在できるスキルミオンは典型的なナノスピン構造です。
我々は、この非一様空間構造を好むカイラル磁性体と光渦の非一様強度分布は相性が良いと推測し、
光渦をカイラル磁性体に照射することで光渦の空間構造が磁性体に「プリント」され、
新しいスピンテクスチャが発生するのではないかと考えました。
しかしこの可能性を理論的に解析する上で、
カイラル磁性体と光渦の間に存在する以下のようなミスマッチに注意しなければなりません。
カイラル磁性体で実現するナノスピン構造体(スキルミオン)は1-100nm(ナノメートル)程度であり、
一方、光渦の照射領域の最少限界(回折限界)は通常その波長程度であり、1-100nmの波長に対応する電磁波は
紫外から可視光領域の周波数の光になります。しかし、磁性体の典型的なスピンダイナミクスの周波数は
テラヘルツ(10^12Hz)からギガヘルツ(10^9Hz)領域にあり、紫外や可視光の周波数はスピンにとって早すぎて
感じ取ることが出来ません。このミスマッチを解決して「光渦らしさ」を磁性体に転写する方法として
以下のような2つのアイディアが考えられます:(1)高周波数(可視以上)領域の光渦を磁性体に照射し、
磁性体を非一様に熱することでナノスピン構造を磁性体に生成する、(2)近年のプラズモニクスの技術により、
光をその回折限界よりはるかに微小な領域に集光することが可能になりつつあることを踏まえて
(実際1000nm程度に絞られたTHz領域の光渦の報告があります)、THzかつナノスケールの光渦を磁性体に照射する、という方法です。
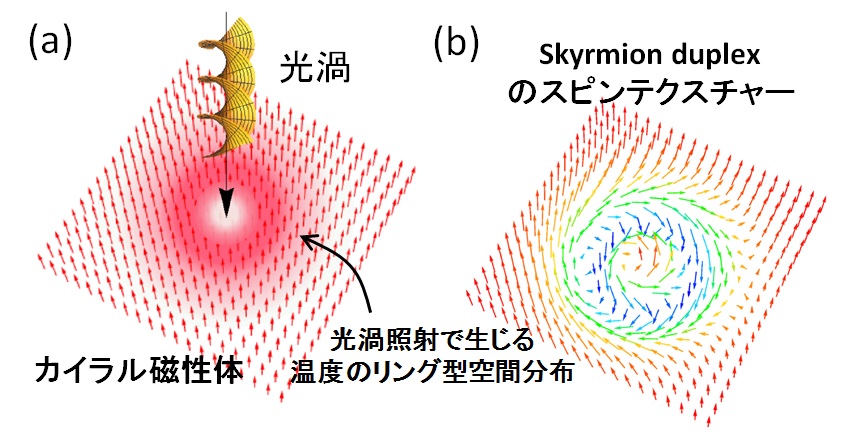
この2つのアイディアに従って、我々は2次元カイラル磁性体に光渦を照射した際に生じるスピン構造(右図(a))を
ランダウ・リフシッツ・ギルバード(LLG)方程式に基づいた数値解析により調べました。
(1)の方法に基づき、光渦の熱効果を数値解析した結果、
スキルミオンと反スキルミオンがドーナツ状に重なり合って出来た新しい磁気欠陥
(Skyrmion Duplexと呼ぶことにする)が光渦により実現可能であることを予言しました(右図(b))。
さらに光渦のリング数やリングの幅を調整することで、
通常のスキルミオンや2重リング構造(Skyrmion Quaduplex)も生成可能であることを明らかにしました。
一方、(2)のTHz光渦を磁性体に照射した場合は、光渦の電磁場とスピンが直接結合する為、
より豊かな物理現象が期待されます。数値解析の結果、THz光渦により、
「多極子的に広がるスピン波」を生成したり、光渦の軌道角運動量の正負や大きさに応じて
異なるトポロジカル磁気欠陥を生成することが可能であることを明らかにしました。
これらの結果は、固体電子系(磁性体)において光渦照射により生じる初めての非自明な現象と言えます。
H. Fujita and M. Sato,
Phys. Rev. B 95, 054421 (2017) selected for an Editors' Suggestion
茨城大解説ページ
H. Fujita and M. Sato,
Phys. Rev. B 96, 060407(R) (2017)
第88回レーザー加工学会論文集記事
非平衡量子系・新しい量子状態の生成・制御
近年、強力なレーザーを量子多体系に照射し平衡系では実現しない非平衡量子状態を生成・制御する研究が急速に進展しています。
レーザー科学が発展していることは上の欄でもすでに述べた通りです。我々は、単純で現実的な量子系である量子磁性体・誘電体・電子系に
レーザーを照射して誘導される新しい物理現象を探索しています。この研究は、上覧で既に述べたスピントロニクスとも密接に関係しています。
実際上で紹介した2つの成果(A1)(A2)も、ここに分類される成果とも言えます。ここでは最近の成果(B1)(B2)について紹介します。
(B1)キタエフハニカム模型におけるレーザー誘起トポロジカルスピン液体状態
キタエフ模型はハニカム格子上で定義されるスピン軌道相互作用の強いモット絶縁体(Ir酸化物など)の有効量子スピン模型です。
この模型は、そもそもキタエフ氏(2006年)が物質科学とは全く関係ない数理物理的動機から提案した模型であり、
基底状態が厳密に表現できるスピン液体状態(秩序がない状態)であり、低エネルギー励起がスピン系であるにもかかわらず
マヨラナフェルミオンで表現される、ということで良く知られています。2009年頃からの欧州グループの研究により、
この人工的な模型がスピン軌道相互作用の強いモット絶縁体の低エネルギー有効模型に成り得ることが指摘され、
物性研究分野におけるこの模型に対する関心が爆発的に高まりました。
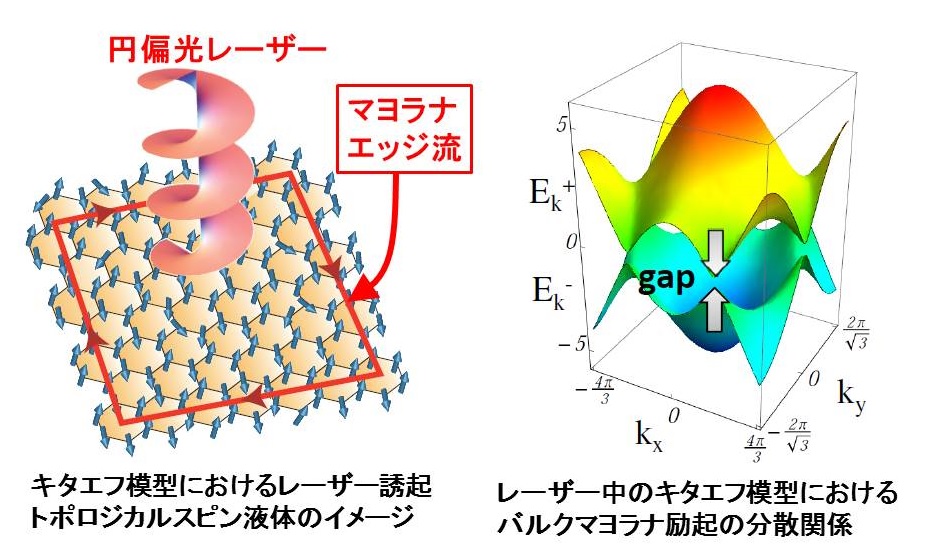
我々はマルチフェロイクス的な電気磁気結合を持つキタエフ模型をフロケ理論に基づいて微視的に解析し、
右(左)巻き偏光レーザーをキタエフ模型に照射すると、ギャップが開き、右(左)回りにマヨラナカイラルエッジ流が流れる
トポロジカルスピン液体(トポロジカルp波超伝導体と等価)が発生することを高周波極限で厳密に示しました。
これは強相関系におけるレーザー誘導トポロジカル量子相の初めての予言といえます。
M. Sato, Y. Sasaki, and T. Oka,
arXiv:1404.2010
佐藤、高吉、岡:日本物理学会2017年11月号に解説記事「レーザー駆動超高速スピントロニクスとフロケエンジニアリング」
(B2)多層グラフェンにおける光誘起エッジ状態
ディラック電子型の分散関係を持つグラフェン(6角格子上に配列した炭素原子による2次元電子系)に円偏光レーザーを照射すると、
レーザーにより新しい虚数因子を持つホッピング項が有効的に誘導されバンドギャップが開き、
エッジ電流が流れるトポロジカル絶縁体相が現れることが予言されています。最近、この予言に対応する実験も実施され、
固体電子系のレーザーによる電子状態の制御に関する研究が発展しています。
このレーザー誘起"相転移"現象は、より一般の2次元格子電子系に応用可能と推測されます。
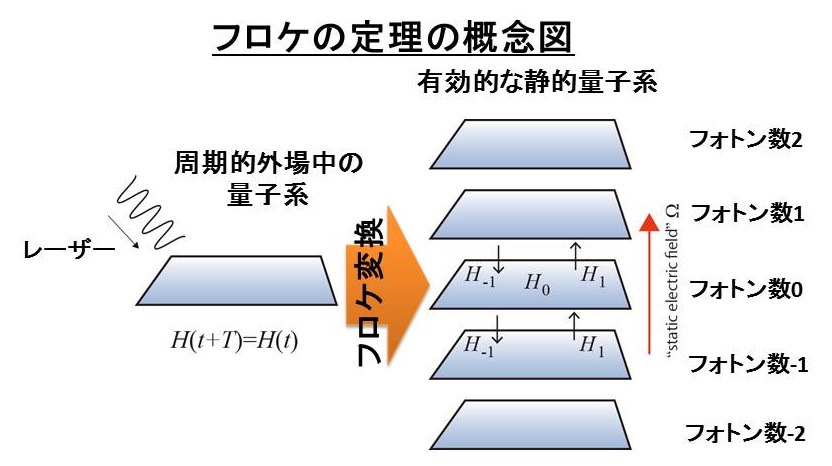
そこで我々は、ディラック電子的分散を持つ多層グラフェン格子上の電子模型に円偏光レーザーを印加した際の有効模型を
フロケの定理と1/Ω展開法用いて導出し、それらの基底状態を解析しました。
その結果、多層グラフェンの種類に応じて多様なエッジ流を持つトポロジカル絶縁相が実現することを明らかにしました。
M. Sato, Y. Sasaki, and N. Furukawa, in preparation.
熱及び光誘起輸送現象・スピン流輸送・ホール効果
熱(温度)と光は、人類が容易に準備・制御できる物性科学における外部パラメータと言えます。
これらをナノ又はマクロスケールの多体系に巧く印加することで生じる物理現象は、
基礎物理学と工学の両観点から注目されており、この設定の中から多くの新しい現象を発見・予言できる可能性があります。
実際、スピントロニクスにおいても、光と熱でスピン流や磁化を生成・制御することは重要な研究テーマと言えます。
(C1)スピンゼーベック効果・スピンポンプ
スピン流(スピン角運動量の流れ)を生成する代表的な方法として、
(1)磁性体に熱勾配を印加してスピン流を生成するスピンゼーベック効果と
(2)適当な周波数(GHzの場合が多い)の光を磁性体に照射してスピン流を生成するスピンポンプ現象が挙げられます。
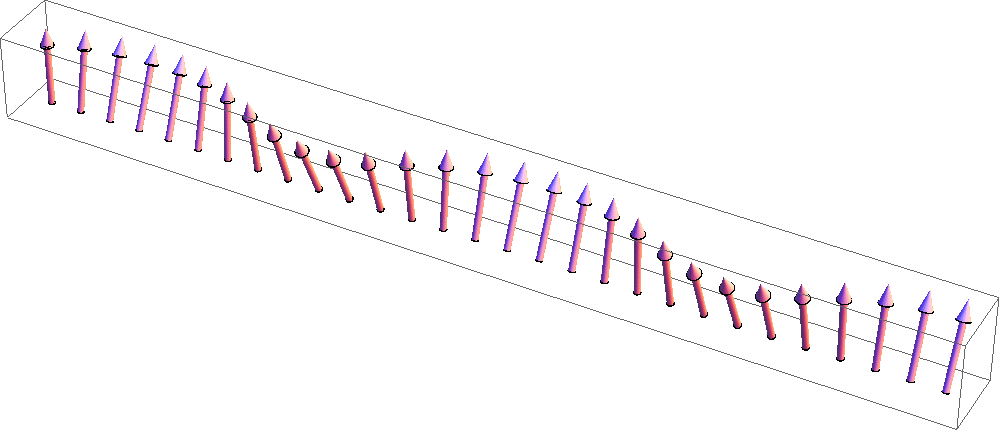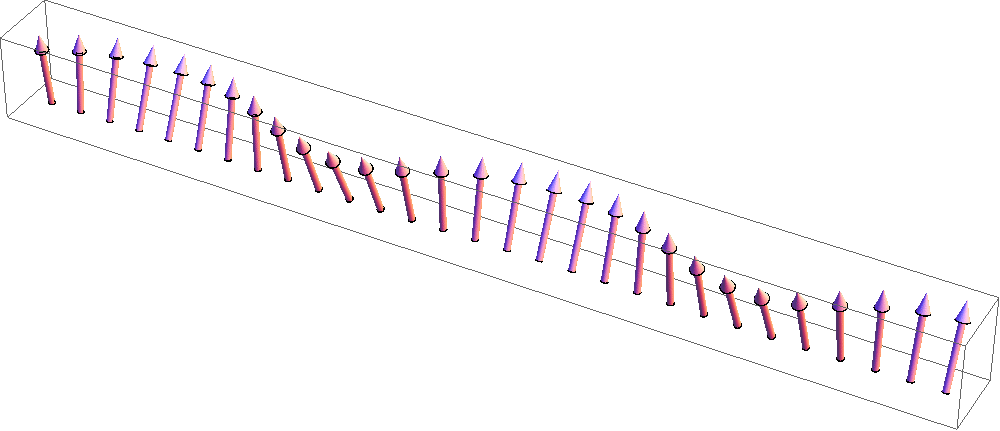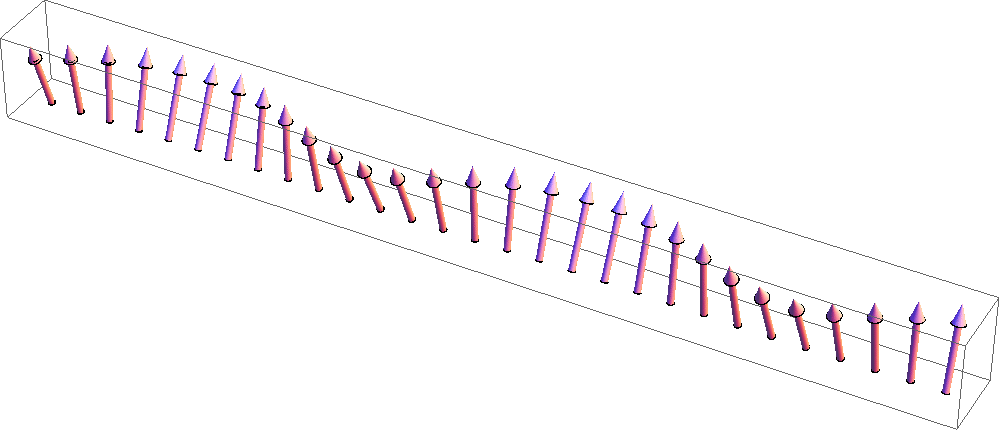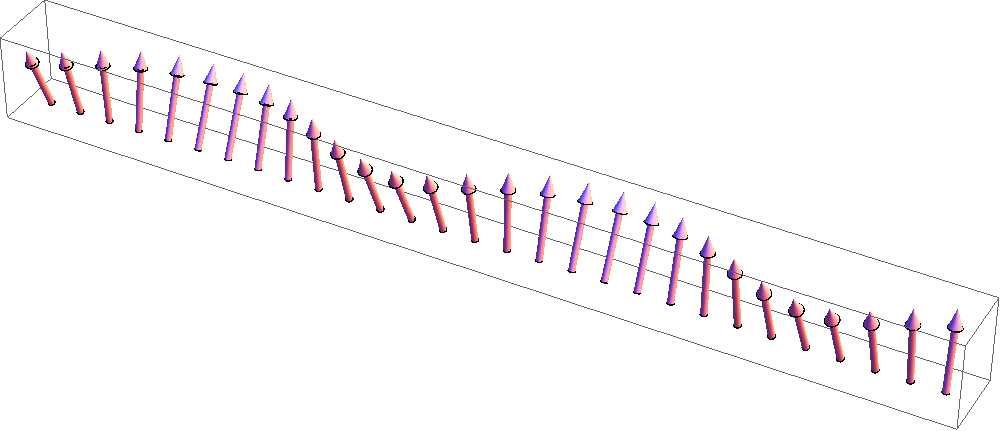
スピントロニクス研究で良く使われるYIG(イットリウム鉄ガーネット)などの強磁性(正確にはフェリ磁性)絶縁体においては、
角運動量を持つ準粒子であるマグノン(右図)がスピン流のキャリアとして働きます。(アニメーション:原子力機構松尾衛氏提供)
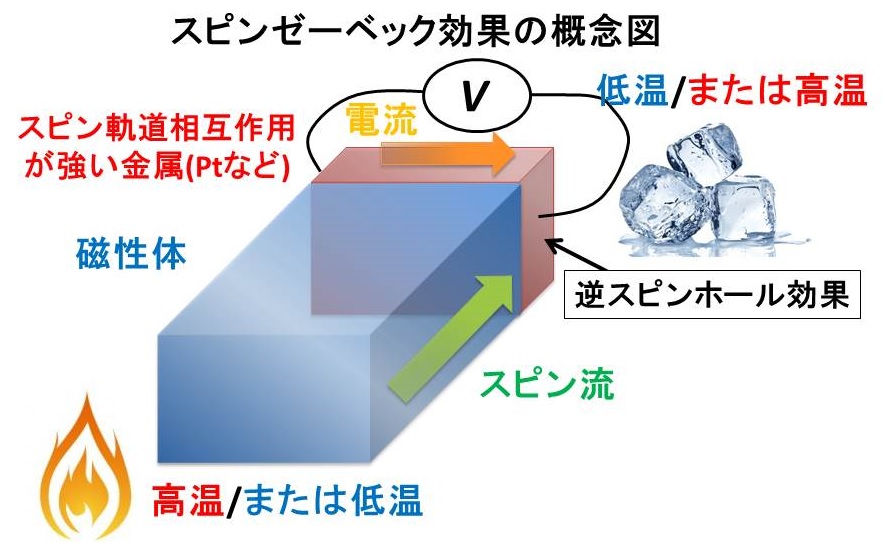
スピンゼーベック効果の実験セットアップは右図のように与えられます。
「対象とする磁性体にスピン軌道相互作用の強い非磁性金属(Ptなど)を接合し、その接合系に温度勾配を与える」
という単純な状況が基本構造です。
温度勾配により磁性体中の準粒子がスピン流を生成し、それが金属に注入されます。
さらに、金属中で生じる逆スピンホール効果を介してスピン流が温度勾配と垂直方向に流れる電流に変換され、
その電圧降下を測定することで磁性体中のスピン流の存在が間接的に確認される、という仕組みです。
スピン流は保存流ではない為直接観測することが困難であり、
それ故金属を接合する点が電子系のゼーベック効果と本質的に異なる点であり、またスピンゼーベック効果の特徴とも言えます。
これまでの磁性絶縁体におけるスピントロニクス研究では、強磁性体とその準粒子であるマグノンの性質に
焦点が当てられてきました。しかしながら、長い歴史を持つ磁性研究から、強磁性体の他に多様な磁気秩序と
磁気的準粒子が実在することが明らかにされています。そこで我々は、強磁性体と極端に対照的な対象である
擬1次元S=1/2量子反強磁性体Sr2CuO3に焦点を当て、そのスピントロニクス機能を調べました。
この系の磁性は反強磁性相関の発達した量子スピン液体(つまり長距離磁気秩序がない)で記述され、
その低エネルギー励起は典型的な分数励起であるスピノン対で支配されていることが、よく知られています。
我々は、この系におけるスピンゼーベック効果の実験を実施し、スピンゼーベック電圧の観測に成功しました。
これは磁気秩序がない混沌とした量子状態におけるはじめてのスピン流の観測であり、またマグノンではない
新しいスピノンスピン流についての初の実験結果でもあります。実際、原子スケールのデバイスを想定するとき、
強磁性秩序をはじめとする磁気秩序は熱・量子揺らぎの効果で破壊され、
一方で量子スピン液体はナノサイズの系でも実在し得ることが理論的に予想されます。
この意味で、量子スピン液体におけるスピントロニクス機能の研究は純粋に理学的な面だけでなく
工学的な意味でも有意義な研究対象と考えることが出来ます。
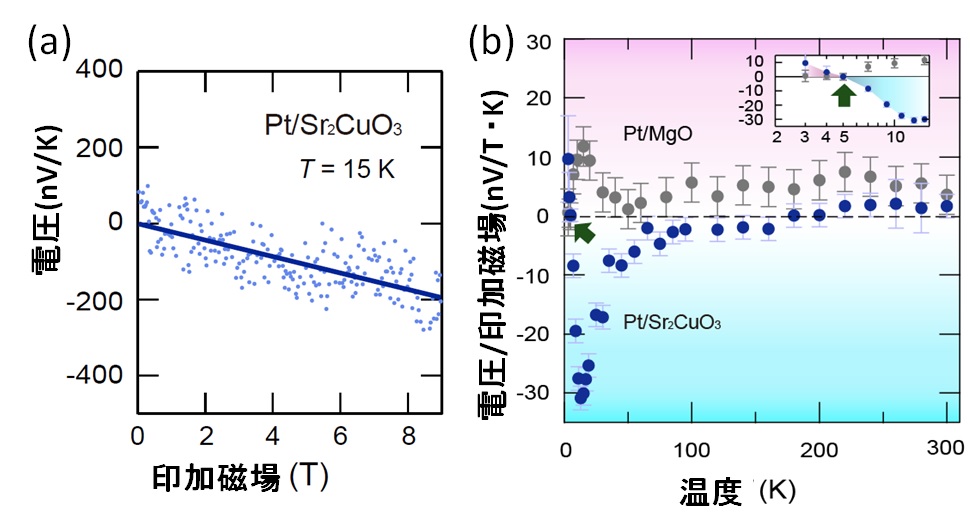
Sr2CuO3の実験結果は右の図に示してあります。
(a)がスピンゼーベック電圧の外部磁場依存性、(b)が同電圧の温度依存性を示しています。
(b)では、比較対象として非磁性物質MgOと金属Ptから成る系のゼーベック電圧(灰色の点)が示されています。
MgO/Ptの系では、Ptで生じるネルンスト効果の影響で正の電圧が観測されていますが、
ターゲットのSr2CuO3/Pt系の結果(青点)は、ネルンスト効果に打ち勝って量子スピン鎖が負の電圧を発生させていることを示唆しています。
2つのパネル(a)(b)から、スピン液体のスピンゼーベック電圧は外部磁場に比例し負の値を示すことが証明されます。
一方、強磁性体のスピンゼーベック電圧は、磁場とともに減少し正符号を取ることが知られており、
我々の研究が、スピノンスピン流がマグノンスピン流と対照的な性質を持つことを明らかにしたと言えます。
我々はこれらのスピノンスピン流の特性を説明する微視的理論の構築にも成功しています。
以上の量子スピン液体におけるスピンゼーベック効果の研究が、急速な発展を遂げているスピントロニクスと
多様な磁気秩序を探求する磁性研究の間の架け橋を与える先駆的な研究になることを期待しています。
現在、1次元量子スピン液体のスピンゼーベック効果の微視的理論についての論文も準備中です。
D. Hirobe, et al, arXiv:1609.06410 and
Nature Physics 13, 30 (2017)
(Online version (2016))
茨城大解説ページ
東北大プレス
原子力機構プレス
M. Sato, et al, in preparation.
Y. Ohnuma, et al, in preparation.
(C2)熱ホール効果
ホール効果は特に物理学で研究対象となる輸送現象です。
広義には、何らかの流れを生成する外部パラメータ(電圧や温度勾配)を印加した方向と垂直方向に流れが誘起される現象を
ホール効果と言ってよいでしょう。ホール効果のset upは一見マニアックに思えますが、
2次元電子系における量子ホール効果の研究を契機に、
ホール伝導度が系の準粒子の波動関数の波数空間におけるトポロジカル(幾何学的)な性質を反映することが広く認識され、
ホール効果は理論物理学に興味深い研究テーマを提供し続けています。磁性絶縁体における準粒子は通常電荷をもたない為、
金属とは異なり、電場では流れを引き起こすことができません。しかしながら、熱勾配を印加すれば磁性絶縁体においても
準粒子のホール効果が起こり得ます。実際、最近の研究により、マグノンによる熱ホール効果が観測されています。
我々は、磁性絶縁体における新しい熱ホール効果の理論を現在構築中です。
E. Takata, and M. Sato, in preparation.
(C3)キタエフ模型候補磁性体RuCl3の熱輸送におけるスピン液体的挙動
量子スピン液体状態を示す量子磁性体の模型の1つとしてハニカム格子上のキタエフ模型が知られています。
キタエフ模型とは、(上の解説でも登場しましたが)ハニカム格子の各格子点に住むスピン1/2によって定義されており、
ハニカム格子の3種類の隣接スピン間ボンドに各々異なるイジング型結合(x,y,z方向のイジング相互作用)が配置されています。
この異方的相互作用が系にフラストレーションをもたらします。この模型はキタエフ氏により厳密に解けるtoyモデルとしてはじめ導入され、
基底状態は磁気秩序をもたないスピン液体になり、(マヨラナ)フェルミオン励起をもつことが知られています。
キタエフ氏の提案の後、キタエフ模型がスピン軌道相互作用が強いモット絶縁体の有効模型に成り得ることが認識され、
キタエフ候補物質の探索やその物性研究が精力的に行われるようになりました。
そのような中で、我々はキタエフ模型候補物質の1つである擬2次元磁性体Alpha-RuCl3に注目しました。
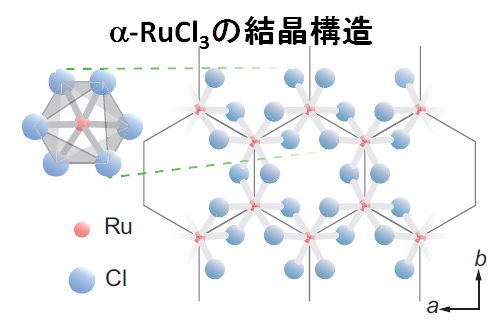
RuCl3は、擬スピン1/2の自由度を持つRuイオンがハニカム格子を形成したスピン軌道相互作用の強いモット絶縁体と考えられています(右図)。
それ故、その磁気的振舞いはキタエフ模型に近いモデルで記述できると期待されています。
実際、比熱や帯磁率などの温度依存性はキタエフ模型に近い挙動を示しています。
純粋なキタエフ模型は絶対零度まで磁気秩序は発現せずスピン液体が実現しますが、
現実の物質であるRuCl3はキタエフ模型からの当然ずれている為、低温で磁気秩序が発生してしまいます。
しかしながら、最近の幾つかの実験は、磁気転移温度より高温側の常磁性相においてRuCl3がフェルミオン的励起を持つことを示唆しています。
そこで我々は、RuCl3のスピン液体的性質を明らかにする為に(さらには新しいスピントロニクス機能を探索する為に)、
この系の熱輸送特性に着目しました。実際、幾つかのスピン液体状態を示すフラストレート磁性体の特徴は
輸送現象により明らかにされています。我々の測定は、RuCl3の熱伝導度の中に高温領域において
磁気的なキャリアによる寄与が有意に存在することを明らかにしました。
これは、RuCl3の高温領域がやはりキタエフ模型に近く、マヨラナフェルミオン的な励起が熱伝導に寄与していること
を示唆する結果と言えます。
D. Hirobe, M. Sato, Y. Shiomi, H. Tanaka, and E. Saitoh,
Phys. Rev. B 95, 241112(R), (2017)
selected for an Editors' Suggestion
不思議な量子相(スピン多極子・ネマティック・カイラリティ)の検出方法の提案、及び固体電子系の電磁場応答の理論
スピン液体、磁気多極子相、カイラリティ秩序相のように複数の局所的演算子の積(又は系全体に渡る演算子の積)で定義される秩序相は、
それらを直接観測する手段が乏しい為、実験でその相を特徴付けることが大変難しいと考えられます。
逆にこれは有効な実験方法が求められていることを意味しているとも言えます。
我々は、それらの相の特徴を巧く実験的に検出する手段を提案することに成功しています。
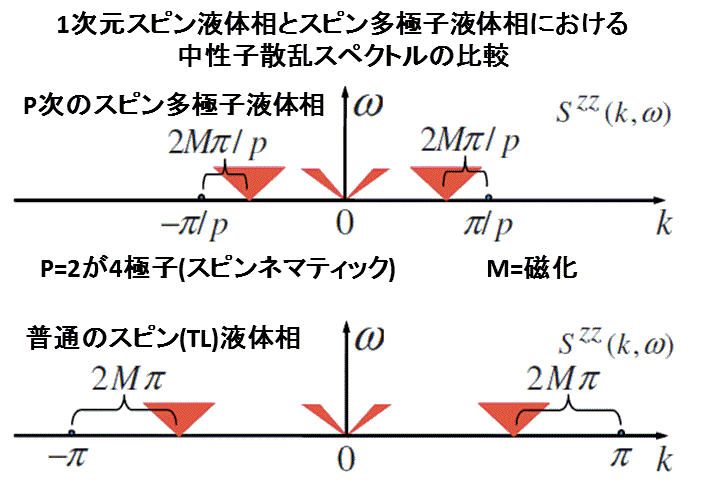
(D1)スピン多極子液体状態の核磁気共鳴(NMR)と中性子散乱による検出方法の提案
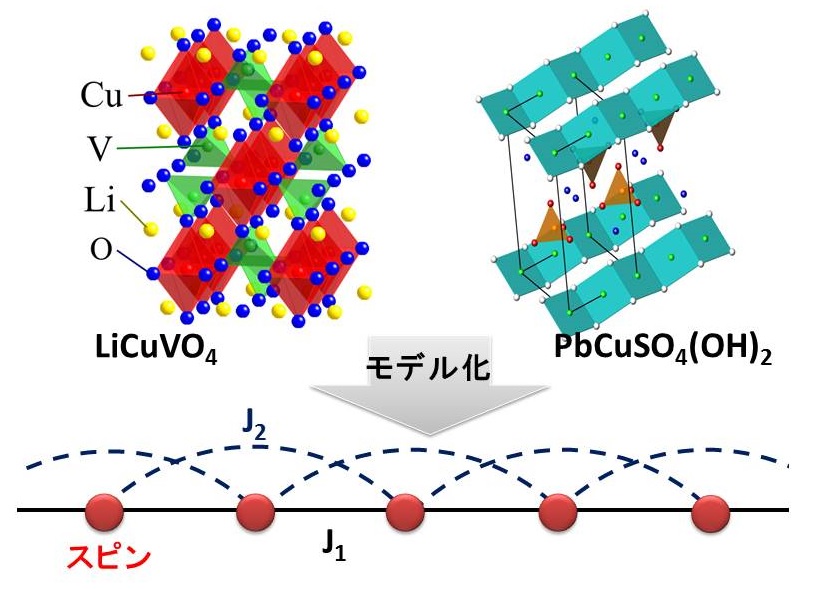
近年、強磁性の最近接相互作用J1と反強磁性の次近接相互作用J2を持つ一連の擬1次元銅酸化物磁性体
(LiCuVO4、Rb2Cu2Mo3O12、PbCuSO4(OH)2など多数:右図)が発見・合成され実験研究が進められています。
この一連の磁性体を記述する有効模型は、最も単純なフラストレート磁性体模型の1つであるJ1-J2スピン鎖模型であることから、
その模型の基底状態相図が多くの理論家によって精力的に解析されました。その結果、磁場中の広いパラメータ領域において
スピン多極子液体相(4極子、8極子、16極子)が現れることが明らかにされました(スピン4極子相をスピンネマティック相とも呼びます)。
そこで我々は、この多極子液体相が実際の磁性体で実現する際に
如何にしてその証拠を検出すればよいか、ということを理論的に考察しました。
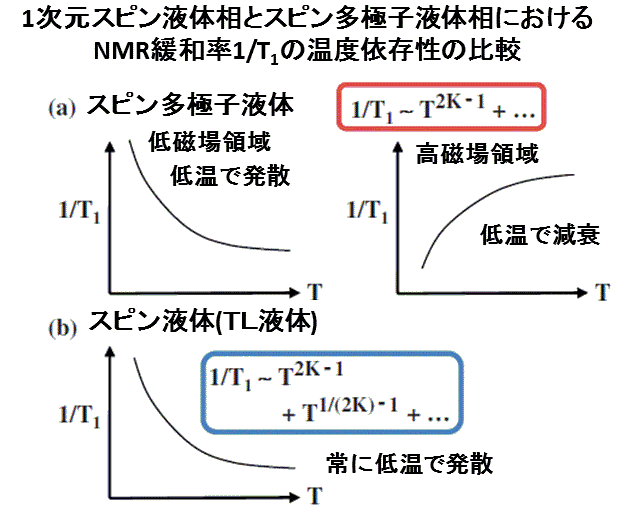
場の理論に基づく考察の結果、多極子液体相の特徴を熱力学量から検出することは難しく、
一方、多極子液体相のユニークな特徴が(1)核磁気共鳴(NMR)の緩和率の温度磁場依存性(右図)と
(2)中性子散乱スペクトルのピーク位置の磁場依存性、に現れることを明らかにしました。
これは磁性体の多極子相に対する初めての現実的実験検出方法の提案であり、
最近LiCuVO4を含む複数個の磁性体の実験でこの予言が実証されています。
M. Sato, T. Momoi, and A. Furusaki, Phys. Rev. B 79, 060406(R) (2009)
selected for an Editors' Suggestion
M. Sato, T. Hikihara, and T. Momoi, Phys. Rev. B 83, 064405 (2011)
M. Sato, T. Hikihara, and T. Momoi, Phys. Rev. Lett. 110, 077206 (2013)
M. Sato, T. Hikihara, and T. Momoi, J. Phys.: Conf. Ser. 320, 012014 (2011)
(D2)マルチフェロイクスにおけるエレクトロマグノン・エレクトロスピノン
マルチフェロイクス(強誘電磁性体)とは、(上の欄でも触れた様に)強い電気磁気結合-交差相関-をもち、
磁場だけでなく電場にも応答する磁性絶縁体です。それ故、マルチフェロイクスの発見以来、
その電場に対する応答は精力的に研究されています。特に磁気秩序(典型的にはスパイラル秩序)を持つマルチフェロイクスにおいて、
外部電場によって電気磁気結合を介して励起されるマグノン励起はエレクトロマグノンと呼ばれています。
我々は、量子性の効果が大きいと思われる低次元性の高いマルチフェロイック物質を対象として、それらの電磁場応答の理論を構築しました。
(1)フラストレートスピン鎖が結合した構造を持つLiCu2O2に対してスピン波理論を展開し、
低エネルギー周波数帯(THzからGHz)で観測されている誘電率スペクトルの複数のピークが、
エレクトロマグノンで説明可能であることを示しました。
(2)パイエルス不安定性とそれに伴う磁気歪型電気磁気効果を持つ擬1次元有機系化合物(TTF-CAなど)の有効格子模型と電気磁気結合の公式を導き、
それらと場の理論・form factor法を組み合わせることで、光学伝導度に1次元量子系特有のスピノンペアによる連続スペクトルが現れ得ることを
予言しました。これはエレクトロスピノンと呼べる励起と言えます。さらに、ソリトンやブリーザ―と呼ばれる励起も光学伝導度に
現れることも指摘しました。
H. Katsura, M. Sato, T. Furuta, and N. Nagaosa, Phys. Rev. Lett. 103, 177402 (2009)
S. Furukawa, M. Sato, Y. Saiga, and S. Onoda, J. Phys. Soc. Jpn. 77, 123712 (2008)
S. Furukawa, M. Sato, and S. Onoda, Phys. Rev. Lett. 105, 257205 (2010)
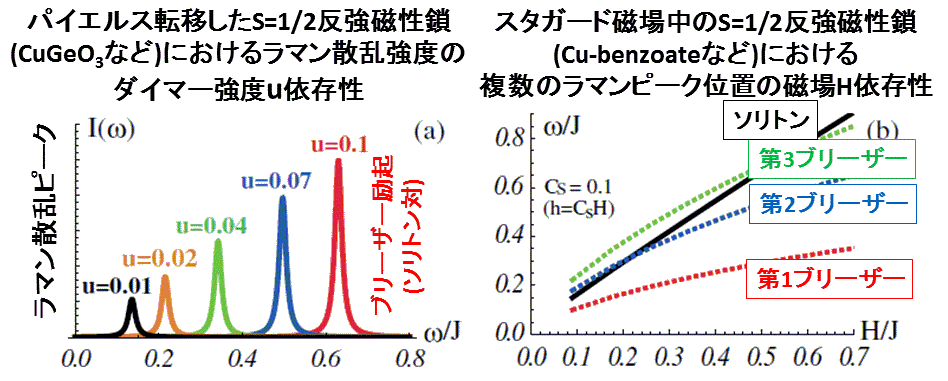
(D3)磁気ラマン散乱による1次元量スピン液体相周辺の特徴付け
ラマン散乱は、物質系と光の間で生じる代表的な散乱過程の1つであり、特に格子振動や分子振動を観測するのに有効であることが知られています。
一方、磁気励起によるラマン散乱も観測可能であり、強磁性体や反強磁性体では、その準粒子であるマグノンがラマン散乱で検出されています。
ところが、3次元の磁気秩序相よりも量子揺らぎが強く秩序が発現しない1次元量子スピン系のラマン散乱の理論は未開拓のままでした。
このような量子・熱揺らぎが強い多体系においてラマン散乱スペクトルを含む動的な物理量を定量的に評価することは一般に難しい問題です。
我々は、1次元量子スピン鎖のラマン散乱スペクトルの解析で生じる理論的困難を、
場の理論と可積分系の方法に基づく精密な方法を用いて克服しました。
その結果、他の実験では検出しにくい微小な摂動項(磁気異方性、ボンドの曲り具合、ダイマー化、など)が
ラマン散乱に本質的影響を与えスペクトルが摂動の種類に依存して激変することを明らかにしました。
すなわち、ラマン散乱の新しい利用方法を提案したと言えます。
M. Sato, H. Katsura, and N. Nagaosa, Phys. Rev. Lett. 108, 237401 (2012)
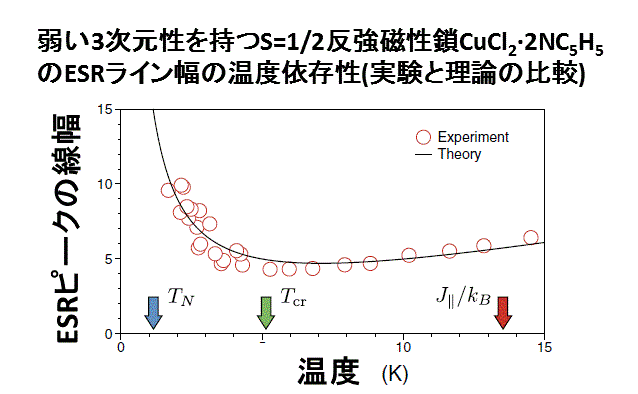
(D4)弱く結合した量子スピン鎖の電子スピン共鳴の理論
電子スピン共鳴(ESR)とは、静磁場中の磁性体に適当な周波数の振動磁場(マイクロ波)を照射して生じる
磁気共鳴現象(古典的にはスピンの歳差運動)を指します。この現象は磁気異方性に敏感であり、
共鳴周波数の値が磁性体が持つ磁気異方性により変化することが知られています。
ESRの微視的理論の研究は、線形応答理論の誕生にまで遡ります。にもかかわらず、上の1次元量子系のラマン散乱と同様に
量子揺らぎが強い1次元量子スピン液体のESR理論は2000年頃まで未開拓のままでした。
2000年前後に発展したOshikawa-Affleck理論をきっかけとして一連の実験・理論研究が精力的に進められ、
1次元量子スピン鎖に対するESRの基礎理論はほぼ完成したと言えます。しかし、多くの1次元性の強い磁性体には
必ず弱いながら有限の3次元性があり、極低温では磁気秩序相(又はスピンギャップ相)が現れることが知られています。
そこで我々は、弱いスピン鎖間の結合も取り込んだESRの理論を場の理論と摂動論を組み合わせて構築しました。
その結果、広いクラスの擬1次元反強磁性体において、鎖間結合の磁気異方性により極低温でESRピークの線幅が広がることを予言しました。
この予言は、幾つかの磁性体で既に観測されている線幅の拡大現象を説明していると考えられます。
S. C. Furuya and M. Sato, J. Phys. Soc. Jpn. 84, 033704 (2015)
(D5)スピン軌道相互作用を持つ1次元トポロジカル絶縁体のエッジ状態の磁気共鳴による検出方法の提案
1次元トポロジカル絶縁体では、一般に系の端に局在したゼロエネルギーを持つエッジ状態が現れます。
この1次元系の典型例としてSu-Schrieffer-Heeger(SSH)模型があり、これはポリアセチレンを最も単純化した模型とみなすことができます。
トポロジカル絶縁相の表面状態は何らかの対称性によって保護されている場合が多く、その対称性を破る摂動に対して
表面状態は一般に不安定です。しかし、摂動が弱いうちは、エッジ状態のエネルギーはゼロからずれるものの、
その波動関数は依然として端近傍に局在していると期待されます。そこで我々は、一様磁場中のスピン自由度を持つSSH模型に対して、
現実的な摂動であるstaggeredなスピン軌道(SO)相互作用と次近接ホッピングを加えた系の端状態を解析しました。
その端状態を電子スピン共鳴(ESR)により検出する方法と磁気共鳴スペクトルの摂動依存性を理論的に考察しました。
外部静磁場と磁気共鳴の振動磁場周波数をバルクバンドギャップ以下のエネルギー領域に絞れば、
ESRの磁気遷移に直接効いてくるのはエッジ状態だけになります。すなわち、この低周波数領域では、ESRスペクトルは
スピンupとdownの2つのエッジ状態間の遷移を見ることになります。
摂動がない場合は、共鳴周波数は単に一様磁場によるゼーマンエネルギーと一致します。
我々は、まず、SSH模型の性質上、最近接のSO結合を入れても共鳴周波数がゼーマンエネルギーからずれないことを厳密に示しました。
続いて、摂動理論を用いて、次近接SO結合を加えたときの共鳴周波数のゼーマンエネルギーからのずれΔωが
コンパクトな解析的表式で表現されることを示し、外部磁場の方向を変化させることでΔωがゼロになる特別な外部磁場の方向が
存在することも明らかにしました。これらの摂動論の結果は、数値計算により直接的に見積もられたΔωの値と
よく一致することも確認できます。これらの結果は、1次元トポロジカル絶縁体のエッジ状態を観測する上で
非常に有効な情報を提供します。
Yuan Yao, Masahiro Sato, Tetsuya Nakamura, Nobuo Furukawa, and Masaki Oshikawa,
Phys. Rev. B 96, 205424 (2017)
フラストレーションや静磁場が誘起する新しい秩序と相転移

磁性体の相転移、相図、フラストレーションに関わる問題は前世紀から研究されている古い分野と言えます。
フラストレーションのある現実的な模型を提案することは比較的容易である為、この手の研究においては
問題設定能力はあまり重要ではありません。一方、与えられた模型の熱平衡状態(基底状態)を如何に求めるか、
という点で理論家の力量が試されます。
(1)相図を求めるというテーマが、長い歴史の中で発展した平衡統計力学の様々な解析方法(場の理論、繰り込み群、変分法、各種展開法、など)
や数値的方法(モンテカルロ法、動的平均場、数値対角化法、密度行列繰込群、など)の格好の応用対象であることと、
(2)何と言っても平衡系の相図は多体系を理解する上での基本中の基本である、ということから
未だに多くの研究者に魅力を与えている分野と言えます。
実際、アイディア次第で現在でも基礎的で興味深いテーマを発掘することもできます。
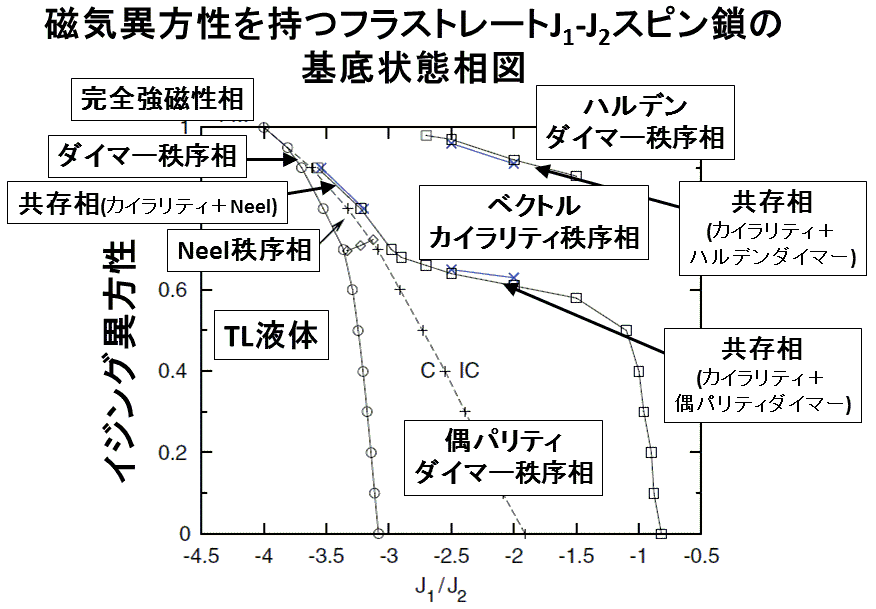
我々はこれまで現実的で単純な模型で起こる多くの新秩序と相転移を明らかにしてきました。
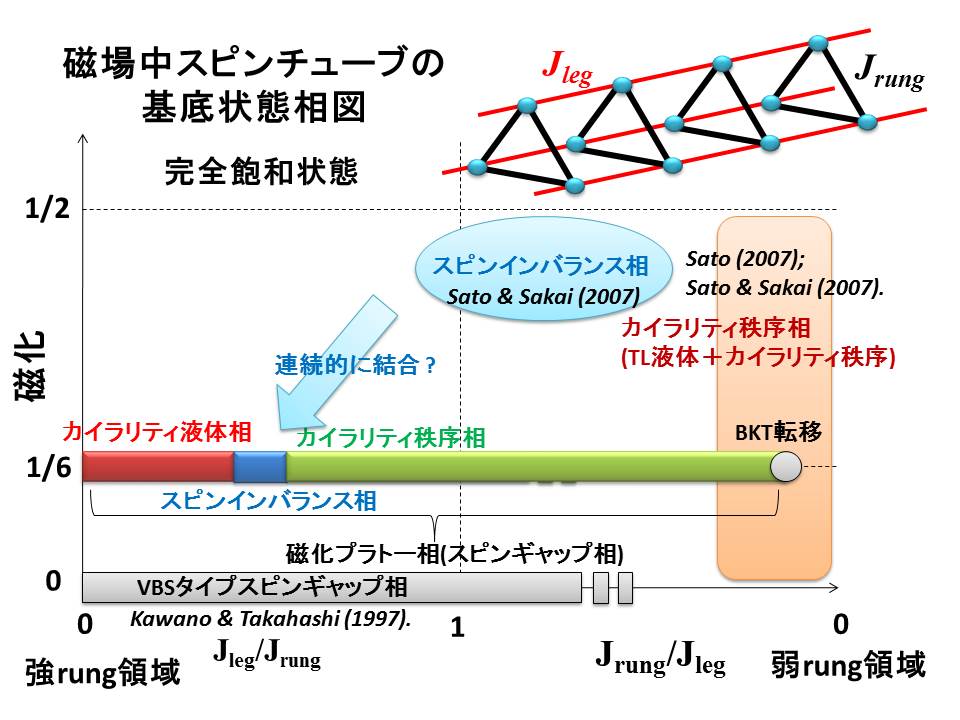
交替磁場が誘導する相転移(Cu-benzoateなど)、ベクトルカイラリティ秩序(ラダー物質など)、
スピンチューブ(CsCrF4など)のカイラリティ液体プラトー相、J1-J2スピン鎖(LiCuVO4など)のNeel-dimer多重相転移とHaldane dimer相、
磁場中3角格子反強磁性体(Cs2CuBr4,Kappa(ET)2Cu2(CN)3など)において弱い摂動で発生するスカラーカイラル秩序やネマティック秩序、
空間異方性のある3角格子イジング模型において微小な次近接相互作用が誘起するキンク励起の準長距離秩序化、
J1-J2スピン鎖が弱く結合した3次元磁性体(LiCuVO4など)において低温で生じるスピン密度波相と
スピンネマティック相を含む定量的な温度磁場相図(右図)などが代表的な成果と言えます。
 M. Sato, and M. Oshikawa, Phys. Rev. B 69, 054406 (2004)
M. Sato, and M. Oshikawa, Phys. Rev. B 69, 054406 (2004)
M. Sato, and T. Sakai, Phys. Rev. B 75, 014411 (2007)
M. Sato, Phys. Rev. B 75, 174407 (2007)
M. Sato, Phys. Rev. B 76, 054427 (2007)
T. Sakai, et al, Phys. Rev. B 78, 184415 (2008)
T. Sakai, et al, Journal of Physics: Condensed Matter 22, 403201 (2010)
K. Okunishi, et al, Phys. Rev. B 85, 054416 (2012)
S. Furukawa, M. Sato, and A. Furusaki, Phys. Rev. B 81, 094430 (2010)
selected for an Editors' Suggestion
M. Sato, S. Furukawa, S. Onoda and A. Furusaki, Modern Physics Letters B Vol. 25, Issues:12-13, pp.901-908 (2011)
S. Furukawa, M. Sato, S. Onoda and A. Furusaki, Phys. Rev. B 86, 094417 (2012)
selected for an Editors' Suggestion
M. Sato, T. Hikihara, and T. Momoi, Phys. Rev. Lett. 110, 077206 (2013)
M. Sato, N. Watanabe and N. Furukawa, J. Phys. Soc. Jpn. 82, 073002 (2013) など
格子上の強相関量子多体模型と単純な場の量子論(共形場理論・可解場の理論)との関係性
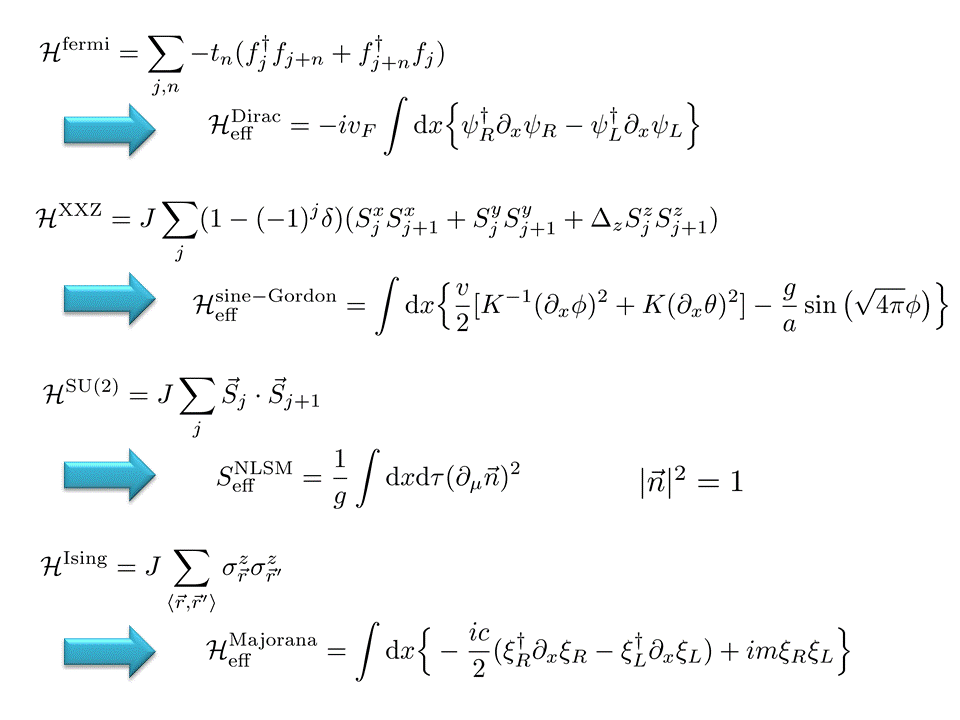
1次元XXZ模型(ハードコアボソン,spinlessフェルミオンと等価)やハバード模型などの単純で基礎的な系の有効理論は、
その系だけでなく摂動を加えた系や1次元鎖が結合した高次元系の定量的な予言を与える際に大変有効であることが知られています。
我々は、格子模型(XXZ模型やラダー)とその有効理論(sine-Gordon理論や共形場理論)との間に存在する関係式
(格子上の演算子の場の理論表示など)やパラメータを決定し、それらの有効性を明らかにしてきました。
以下、2つの結果について紹介します。
(F1)可積分場の理論を活用した格子系と連続極限理論の演算子間等式の決定
我々の研究以前に、代表的な1次元格子上の量子模型において、格子系の局所演算子と
その場の理論表示の間を結ぶ係数(形状因子)の定量的決定方法として、
数値的に求めた局所演算子の2点関数の漸近形を利用する方法が確立していました。
我々は、この方法とは独立に、
(1)わざわざ考察したい格子模型に適切な摂動を加えて、対応する連続極限が可積分場の理論になるように調整し、
(2)可積分理論の厳密に知られている励起スペクトルと数値的に求めた変形格子模型の励起構造を比較することで、
元の模型と対応する場の理論の関係を決定する方法を開発しました。
我々の方法では、既に確立している方法とは異なり系の長距離の性質を必要としない為、
軽い数値計算で信頼できる結果を得られるという利点があります。
S. Takayoshi, and M. Sato, Phys. Rev. B 82, 214420 (2010)
(F2)非線形シグマ模型と整数スピン反強磁性鎖の関係の擬1次元系への応用
1次元整数スピン反強磁性体はスピンギャップのある無秩序な基底状態(ハルデンギャップ相という)を持ち、
その低エネルギー有効模型が可積分のO(3)非線形シグマ模型で与えられることが良く知られています。
定量的な数値解析と場の理論に基づく研究から、非線形シグマ模型に含まれる結合定数、スピン波速度、繰り込み因子などの
少数のパラメータが元の1次元格子上の反強磁性体のパラメータ(スピンの大きさSと交換相互作用J)の関数として定量的に見積もられています。
我々は、これらの精密な情報と可積分系のform factor理論を応用して、
任意の格子上の交換相互作用で弱く結合した任意の本数の整数スピン反強磁性鎖の低エネルギーマグノン励起スペクトルを
定量的に与える理論(鎖間結合に対する摂動論)を構成しました。さらに、この理論から、
2又は3次元的に弱く結合した整数スピン反強磁性鎖のハルデンギャップが閉じる量子相転移点の見積りにも成功しました。
M. Sato, and M. Oshikawa, Phys. Rev. B 75, 014404 (2007)
関連論文:M. Sato, Phys. Rev. B 72, 104438 (2005).
M. Sato, J. Stat. Mech. (2006) P09001
冷却原子系特有の物理現象
冷却原子系は比較的最近実現した人工的な量子力学系です。
大量の原子をレーザーを用いてトラップすることが可能であり、そのような系は量子多体系と見做すことができます。
すなわち、トラップされた冷却原子気体は、身近に存在する固体、液体、気体系とは別の新しい量子多体系の舞台を提供しています。
冷却原子気体系では、空間次元性、格子の形状、相互作用の強さ、内部自由度などを自在に変化させることができ、
これは固体電子系にはない優れた特性です(この特性に甘えて、人工的な模型を解く理論研究が大量発生してしまった、という側面もあります)。
一方で、その実験手段はまだまだ貧弱であり測定できる物理量も非常に限られます。
長い歴史を持つ固体物性研究の実験手段の方が、精度・手軽さ・種類などの面で圧倒的に優れています
(実際、世界中で数えるほどの研究グループでのみ冷却原子気体の実験が可能です)。
従って、冷却原子の量子多体系の理論研究をするのであれば、固体電子系の真似をするのではなく
冷却原子系ならではの切り口を見つけ出すことが研究の価値を高める上で重要だと個人的に感じます。
このような志に見合う成果は今のところ出せていませんが、我々はこれまでの研究で、固体では実現し難い幾つかの予言を得ています。
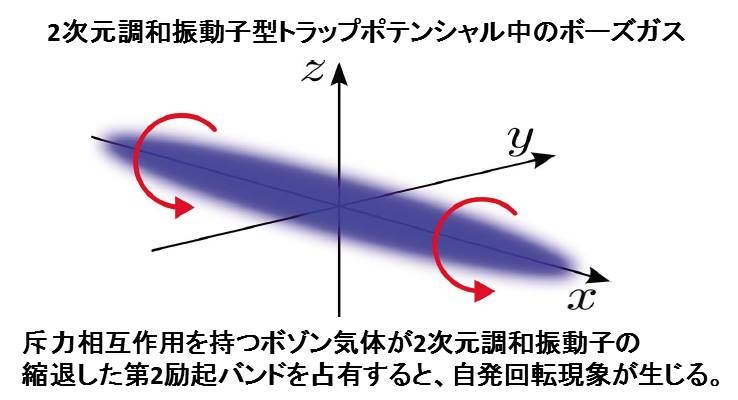
(a)葉巻型ボーズガスにおいて、閉じ込めポテンシャルの強さと粒子数密度が誘起する自発的回転現象の予言。
(b)2成分ボーズ・フェルミガスにおいて、異成分間斥力が誘導する自発的に成分間密度差が発生した
インバランス相(強磁性液体相ともいえる)へ量子相転移の解明。(c)一般の奇数成分(3成分以上)の1次元原子ガス系において、
異成分間ホッピングと異成分間斥力が引き起こす自発ループ流秩序と原子密度の3重積秩序を持つ新量子状態の予言。
(d)3次元スピン1ボーズガスの2種類の4極子相におけるスペクトル関数と密度及びスピン動的構造因子の波数・振動数依存性の解析、
及びそれら構造因子による2種の4極子相の特徴付け。
A. Tokuno and M. Sato, Phys. Rev. A 78, 013623 (2008)
S. Takayoshi, M. Sato, and S. Furukawa, Phys. Rev. A 81, 053606 (2010)
T. Suzuki, and M. Sato, arXiv:1505.06592 など




















 M. Sato, and M. Oshikawa,
M. Sato, and M. Oshikawa,